Defense Against the Dark Arts: the Reverse Regression Effect

Much like our harmonious world, imagine a world populated with blue and green men living as brothers, ignoring the difference of the color of their skin. Much like our exciting world, both blue and green men get educated, go into the real world, and get jobs. One day, a green activist tells you that according to a recent study, for every given education level, blue men receive much higher salary on average than green men, a clear sign of discrimination against the greens — why should equally educated green men not be paid as much as blue men? After leaving you indignant and disappointed, a blue activist tells you that according to another study, for every salary level, green men are less educated than blue men, a clear sign of discrimination against the blues — why should blue men study harder in school than green men to get the same rewards for their work?

The punchline, of course, is that the two studies come from the same data. Judea Pearl mentions it as a throwaway comment in a general talk “The Art and Science of Cause and Effect,” which I read in his great work Causality. In particular, the paper referenced was Goldberger’s 1984 paper Reverse Regression and Salary Discrimination, with actual data demonstrating the effect (though with a different color palette). I find it surprising that Pearl would dedicate an entire chapter in Causality to Simpson’s Paradox but only one comment in the talk to this effect. While it is somewhat similar to Simpson’s Paradox (which I may talk about some other time), they are decidedly different in origin and I find this phenomenon much more relevant, prominent, and chilling. Let me explain.

“You must have set it up wrong.”

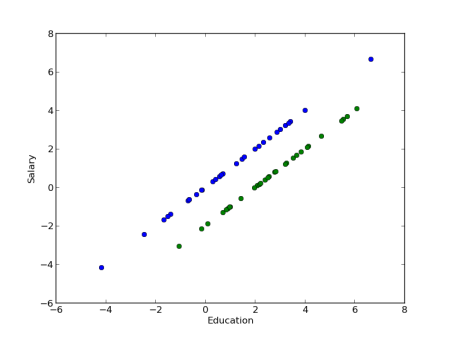
I’ve heard this comment several times already. The argument goes something like this: unless the data is really pathological, we can assume the data is something like a curve for each blue and green on the education vs. salary plot. Let’s say that education is the x-axis and salary the y-axis. The first report shows that in general we need to have the blue curve above the green curve at all vertical slices of the graph. But this means the blue curve must be left of the green curve at all horizontal slices of the graph, which contradicts the second report.

Like all other examples of good math done in the wrong situations, the problem lies not with the logic above (which is correct) but with the assumptions. Instead, let’s make another very commonplace generative model:

• assume the employers were just and higher education corresponds to higher salary, and there is no discrimination at all; (equivalently, have the education vs. salary plot be centered on the x=y line)
• for whatever reason, have the blue men be more educated than the green men and thus get more salary (this could be, of course, due to prior discrimination in the history of the world, socioeconomic circumstances, etc. But the point is we don’t have that kind of information in our data. That’s why I stressed that the employers were just and not the world).
• important: add some noise. So we don’t have well-defined lines, but some variation in ability and occasional misplacement of salary to ability.

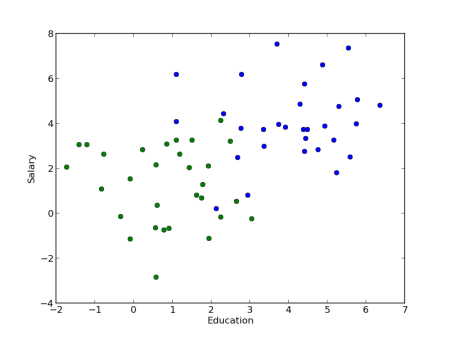
This gives you a graph that looks more like the following:

And now you see it — on vertical slices, blue tend to be higher; on horizontal slices, blue tends to be on the right, something that we thought was very counter-intuitive due to the “lines” model. As Boris Alexeev pointed out to me, the noise is actually doing all of the work in this model!

The watchful reader will notice that this model makes very few assumptions and is very natural, and surely he/she can make some ideas of real-world data that follows this pattern. This is one main difference between the reverse regression effect and Simpson’s Paradox — by some fairly natural definition of “random,” a random set of data will get into the Simpson’s Paradox situation about 1/60 of the time (see Pearl). The RRE  does not depend on such coincidences.

Interpretations and Discrimination

So what is really going on? Some people get very impatient at this point: “is there discrimination or is there not?” Well, whether you believe my simple generative model or not, what is objectively going on is just that the data is telling a very simple story, which is that A) blue men are more educated and B) more educated people get paid more. Sadly, by trying to torture the data to make it talk, we are overstepping our bounds on what we can extract from the data. What the two activists are doing is trying to pull some complicated mechanism, like discrimination, out in a contorted way from very simple data.

An obvious question to ask at this point is: “how do we tell when discrimination exists?” Well, discrimination is a complicated object and it could come in different forms, including, say:

• discrimination-1: employers get equally qualified people, but then pay them less if they were green men
• discrimination-2: employers are just, but the blue people discriminated against green people earlier and green men were put in tough socio-economical situations
• discrimination-3: …

The point is finding different kinds of discrimination is different, but we have an overloaded (and very emotionally charged!) word “discrimination.” To really find discrimination, you have to define each carefully and look for them separately. Using Pearl’s language, I would outline all different types of discrimination as different causal mechanisms. (formally, this means different graphical models using Pearl’s approach) I would then look at the world and see if those models make sense for the data. Qualitatively, it means something we knew intuitively all along: we need more history about this blue-green world and see how it compares with other worlds: maybe in most other worlds the green men are equally educated as blue men; maybe in this world the education of green men were repressed a century ago and education level has a hereditary effect. In our situation, a careful statement would be something like:

• discrimination-1: we don’t see discrimination-1, rather evidence against it;
• discrimination-2: we don’t see it, but we don’t see evidence against either. We don’t have the right kind of data to find discrimination-2.
• discrimination-3: … 

Yes, reductionism makes it more complicated. But it is necessary if we need to make precise judgments.

Epilogue: the Dark Arts

Why did I mention the Dark Arts? Can this information be maliciously used? Hell yes. I’ve literally just given you a recipe to finagle the politically charged idea of discrimination, GOING BOTH WAYS, from a single set of data. So if you feel like it, you can take basically any reasonable population story and create a perfectly-reasonable-sounding discrimination case against either side! I can even go a step further and see a use case when someone can point to this very effect to claim that no discrimination has taken place in a world where it really did (for example, maybe discrimination has actually caused the blue-green difference in education in the first place)! It is very important to stress that the RRE does not show that discrimination does not exist, rather that similar data like this example alone does not show discrimination. If this commonplace but nuanced situation is not Dark Arts (the knowledge of which is prerequisite to defend against it) of mathematics, I don’t know what is. The only thing I can do is to use this knowledge responsibly;  I hope it has similarly helped you.

Thanks to Boris Alexeev for first pointing me towards this effect and Pearl’s work on Causality. It was one of the best time investments I’ve ever made for mathematics.

-Yan